알고리즘을 실행하는데 걸리는 시간을 표현하면 다음과 같다.
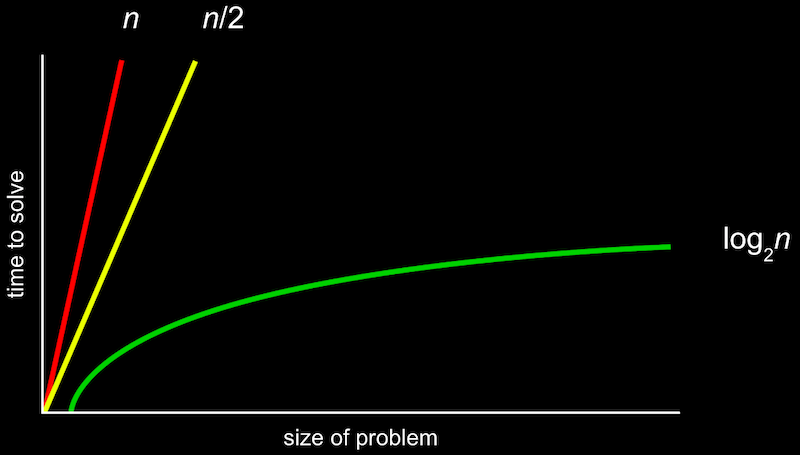
위와 같은 그림을 공식으로 표기한 것이 Big O 표기법이다.
여기서 O는 “on the order of”의 약자로, 쉽게 생각하면 “~만큼의 정도로 커지는” 것이라고 볼 수 있다.
O(n) 은 n만큼 커지는 것이므로 n이 늘어날수록 선형적으로 증가하게 된다. O(n/2)도 결국 n이 매우 커지면 1/2은 큰 의미가 없어지므로 O(n)이라고 볼 수 있다.
주로 아래 목록과 같은 Big O 표기가 실행 시간을 나타내기 위해 많이 사용된다.
- O(n^2)
- O(n log n)
- O(n) - 선형 검색
- O(log n) - 이진 검색
- O(1)
Big O가 알고리즘 실행 시간의 상한을 나타낸 것이라면, 반대로 Big Ω는 알고리즘 실행 시간의 하한을 나타내는 것이다.
예를 들어 선형 검색에서는 n개의 항목이 있을때 최대 n번의 검색을 해야 하므로 상한이 O(n)이 되지만 운이 좋다면 한 번만에 검색을 끝낼수도 있으므로 하한은 Ω(1)이 된다.
역시 아래 목록과 같은 Big Ω 표기가 많이 사용된다.
- Ω(n^2)
- Ω(n log n)
- Ω(n) - 배열 안에 존재하는 값의 개수 세기
- Ω(log n)
- Ω(1) - 선형 검색, 이진 검색
선형 검색
찾고자 하는 자료를 검색하는 데 사용되는 다양한 알고리즘이 있다. 그 중 하나가 선형 검색이다.
선형 검색은 원하는 원소가 발견될 때까지 처음부터 마지막 자료까지 차례대로 검색한다.
이렇게 하여 선형 검색은 찾고자 하는 자료를 찾을 때까지 모든 자료를 확인해야 한다.
선형 검색 알고리즘은 정확하지만 아주 효율적이지 못한 방법이다.
리스트의 길이가 n이라고 했을 때, 최악의 경우 리스트의 모든 원소를 확인해야 하므로 n번만큼 실행된다.
여기서 최악의 상황은 찾고자 하는 자료가 맨 마지막에 있거나 리스트 안에 없는 경우를 말한다.
만약 100만 개의 원소가 있는 리스트라고 가정해본다면 효율성이 매우 떨어짐을 느낄 수 있다.
반대로 최선의 상황은 처음 시도했을 때 찾고자 하는 값이 있는 경우이다.
평균적으로 선형 검색이 최악의 상황에서 종료되는 것에 가깝다고 가정할 수 있다.
선형 검색은 자료가 정렬되어 있지 않거나 그 어떤 정보도 없어 하나씩 찾아야 하는 경우에 유용하다.
이러한 경우 무작위로 탐색하는 것보다 순서대로 탐색하는 것이 더 효율적이다.
버블 정렬
정렬되지 않은 리스트를 탐색하는 것 보다 정렬한 뒤 탐색하는 것이 더 효율적이다.
정렬 알고리즘 중 하나는 버블 정렬이다.
버블 정렬은 두 개의 인접한 자료 값을 비교하면서 위치를 교환하는 방식으로 정렬하는 방법을 말한다.
버블 정렬은 단 두 개의 요소만 정렬해주는 좁은 범위의 정렬에 집중한다.
이 접근법은 간단하지만 단 하나의 요소를 정렬하기 위해 너무 많이 교환하는 낭비가 발생할 수도 있다.
아래와 같은 8개의 숫자가 임의의 순서로 나열되어 있다.
이 숫자들을 오름차순으로 정렬하기 위해 바로 옆의 있는 숫자들과 비교하는 방법을 사용해 본다.
6 3 8 5 2 7 4 1
먼저 가장 앞의 6과 3을 비교해서 순서를 바꾼다.
교환 전: 6 3 8 5 2 7 4 1
교환 후: 3 6 8 5 2 7 4 1
다음 쌍인 6과 8을 비교해보면 교환할 필요가 없으므로 그대로 둔다.
바로 다음에 있는 쌍인 8과 5를 비교해서 순서를 바꾼다.
교환 전: 3 6 8 5 2 7 4 1
교환 후: 3 6 5 8 2 7 4 1
이런 식으로 숫자 끝까지 진행하면 아래와 같이 정렬이 된다.
3 6 5 2 7 4 1 8
하지만 아직 오름차순으로 정렬이 되지 않았기 때문에, 다시 처음부터 동일한 작업을 반복한다.
3 6 5 2 7 4 1 8
3 6 5 2 7 4 1 8 (교환)
3 5 6 2 7 4 1 8 (교환)
3 5 2 6 7 4 1 8
3 5 2 6 7 4 1 8 (교환)
3 5 2 6 4 7 1 8 (교환)
3 5 2 6 4 1 7 8
조금 더 잘 정렬이 되었다. 이 과정을 끝까지 반복하면 최종적으로 아래와 같이 오름차순 정렬이 된다.
1 2 4 3 5 6 7 8
이러한 정렬 방식을 ‘버블 정렬’이라고 한다.
마치 거품이(비교 및 교환이) 터지면서 위로 올라오는 (배열의 옆으로 이동하는) 방식이기 때문이다.
선택 정렬
보통 배열이 정렬되어 있으면 정렬되지 않은 배열보다 더 쉽게 탐색할 수 있다.
정렬을 위한 알고리즘 중 선택정렬을 배열 안의 자료 중 가장 작은 수(혹은 가장 큰 수)를 찾아 첫 번째 위치(혹은 가장 마지막 위치)의 수와 교환해주는 방식의 정렬이다.
선택 정렬은 교환 횟수를 최소화하는 반면 각 자료를 비교하는 횟수는 증가한다.
다음과 같은 정렬되지 않은 숫자들을 오름차순 정렬해본다.
6 3 8 5 2 7 4 1
먼저 아래 숫자들 중에서 가장 작은 값을 찾는다.
6 3 8 5 2 7 4 1
가장 작은 값인 1은 가장 앞에 있어야 하므로 현재 리스트의 첫 번째 값인 6과 교환한다.
1 3 8 5 2 7 4 6
그리고 정렬되어 있는 1은 제외하고, 두 번째 숫자부터 시작해서 또 가장 작은 값을 찾는다.
1 3 8 5 2 7 4 6
가장 작은 값인 2는 정렬되지 않는 숫자들 중에서 가장 앞에 있어야 하므로 3과 교환한다.
1 2 8 5 3 7 4 6
이 과정을 더 이상 교환이 일어나지 않을때까지 반복하면, 아래와 같이 오름차순 정렬이 완료된다.
1 2 3 4 5 6 7 8
이러한 정렬 방법을 ‘선택 정렬’ 이라고 한다.
병합 정렬
병합 정렬은 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가며 정렬을 하는 방식입니다.
그리고 이 과정은 재귀적으로 구현된다
다음 숫자들을 오름차순으로 정렬해 본다.
7 4 5 2 6 3 8 1
먼저 숫자들을 반으로 나눈다.
7 4 5 2 | 6 3 8 1
그리고 나눠진 부분 중 첫번째를 한번 더 반으로 나눈다.
7 4 | 5 2 | 6 3 8 1
마지막으로 한 번 더 나눈다.
7 | 4 | 5 2 | 6 3 8 1
이제 숫자가 두 개 밖에 남지 않았으므로 더 이상 나누지 않고, 두 숫자를 다시 병합한다.
단, 이 때 작은 숫자가 먼저 오도록 한다. 4와 7의 순서를 바꿔서 병합하는 것이다.
4 7 | 5 2 | 6 3 8 1
마찬가지로 5 2 부분도 반으로 나눈 후에 작은 숫자가 먼저 오도록 다시 병합할 수 있다.
4 7 | 2 5 | 6 3 8 1
그럼 이제 4 7과 2 5 두 개의 부분들을 병합한다.
각 부분들의 숫자들을 앞에서 부터 순서대로 읽어들여 비교하여 더 작은 숫자를 병합되는 부분에 가져온다.
즉, 4와 2를 먼저 비교해서 2를 가져옵니다. 그 후에 4와 5를 비교해서 4를 가져온다.
그리고 7과 5를 비교해서 5를 가져오고, 남은 7을 가져온다.
2 4 5 7 | 6 3 8 1
이제 남은 오른쪽 4개의 숫자들도 위와 동일한 과정을 거친다.
2 4 5 7 | 1 3 6 8
마지막으로 각각 정렬된 왼쪽 4개와 오른쪽 4개의 두 부분을 병합한다.
2와 1을 비교하고, 1을 가져옵니다. 2와 3을 비교하고, 2를 가져온다. 4와 3을 비교하고, 3을 가져온다.
4와 6을 비교하고… 이 과정을 병합이 끝날때까지 진행하면 아래와 같이 정렬이 완료된다.
1 2 3 4 5 6 7 8
전체 과정을 요약해서 도식화해보면 아래와 같다.
7 | 4 | 5 | 2 | 6 | 3 | 8 | 1 → 가장 작은 부분 (숫자 1개)으로 나눠진 결과이다.
4 7 | 2 5 | 3 6 | 1 8 → 숫자 1개씩을 정렬하여 병합한 결과이다.
2 4 5 7 | 1 3 6 8 → 숫자 2개씩을 정렬하여 병합한 결과이다.
1 2 3 4 5 6 7 8 → 마지막으로 숫자 4개씩을 정렬하여 병합한 결과이다.
이러한 방법을 ‘병합 정렬’ 이라고 합니다.
병합 정렬 실행 시간의 상한은 O(n log n) 이다.
숫자들을 반으로 나누는 데는 O(log n)의 시간이 들고, 각 반으로 나눈 부분들을 다시 정렬해서 병합하는 데 각각 O(n)의 시간이 걸리기 때문이다.
실행 시간의 하한도 역시 Ω(n log n) 이다. 숫자들이 이미 정렬되었는지 여부에 관계 없이 나누고 병합하는 과정이 필요하기 때문이다.
출처
https://www.boostcourse.org/cs112/lecture/119035/?isDesc=false
모두를 위한 컴퓨터 과학 (CS50 2019)
부스트코스 무료 강의
www.boostcourse.org
'Programming > 온라인 교육' 카테고리의 다른 글
| [CS50] 포인터 (0) | 2021.12.06 |
|---|---|
| [CS50] 메모리 (0) | 2021.12.06 |
| [CS50] 문자열 (0) | 2021.12.02 |
| [CS50] 컴파일링 (0) | 2021.12.02 |
| [CS50] C언어 (0) | 2021.11.30 |



